3. Developments To-Date for a Benefits Measurement Framework

3.1 Introduction

Several papers have been identified as containing basic theoretical and conceptual discussions underlying the proposed approach to evaluating benefits of freight-transportation improvements. The number of key papers is small, because the great preponderance of the work on highway benefit-cost analysis does not give detailed attention to issue of improvements for freight carriage. And, even where benefits to freight carriage are addressed, the treatment is usually incomplete, since effects of shippers' longer-run responses to lower freight costs are not, in most of the literature, addressed.

There have been three strands of development since 1969 in the development of a cost-benefit analysis framework for transportation investment. Foundational work by Mohring [6] and others set the stage for cost-benefit analysis of transport projects. Two later HLB studies, NCHRP 342 [3] and NCHRP 2-17(4) [2] took these basic principles and applied them to quantify improvements in freight productivity. All three strands are reviewed briefly here. The proposed framework that is described in Section 4 builds on all these elements.

If only we could measure a business firm's short-, medium- and long-run demand schedules for a transport service, these would reveal all of the benefits it and (but with important qualifications) its customers would derive from cost-lowering transport improvements experienced by the carriers on which the firm relies. Indeed, if marginal-cost full prices[5] were charged users of an economy's transport facilities and if all of the economy's markets conformed to the competitive model of economics texts, all of the benefits improvements confer on carriers and, indirectly, their customers could be determined from carriers' demand schedules for just the improved facility; examining the markets for other transport facilities and for commodities that are affected by the improved facility would be unnecessary.

In a world of universal marginal-cost prices and easily determined market demand schedules, benefit measurement would be a simple task. Section 3.2 justifies this assertion for a competitive world. While, for expositional brevity, we write there only about road improvement, this discussion applies without appreciable modification to any transport-facility improvement.

In Section 3.3, we relax Section 3.2's assumption of universal marginal-cost pricing. Without "price equals marginal cost," benefit estimation is much more complex than in 3.2's world.

If elements of monopoly exist in markets for transported commodities, transport demand schedules can yield distorted benefit measures. Section 3.3 shows that, with universal marginal-cost pricing, all of the net benefits that result from improving one of a pair of roads that provide substitute services can be measured using only data from the improved road. Not so in the absence of marginal-cost pricing; improving one road could result in net benefits and costs in road markets other than those for the improved road's services. Section 3.3 also describes both the modifications to Section 3.2's benefit-measurement theory necessary to deal with the absence of marginal-cost pricing and the ways in which real-world data can be used to quantify benefits when marginal-cost pricing is the exception rather than the rule.

3.2 Benefit/Cost Analysis in a World of Marginal-Cost Pricing

This section deals with an economy in which marginal cost prices prevail not only in such private markets as those for autos, apples, and gizmos, but also for such governmentally provided services as roads, airports, and air-traffic control. In competitive markets, marginal-cost prices come about without outside intervention. Each buyer or seller plays so small a role in each market that they all regard market prices as beyond their control.

If the prices of governmentally provided services equal their marginal costs, they do so because the responsible governmental authorities choose to set prices that way. The dominant cost of using most government-provided transport facilities is congestion. This being the case, our analysis here ignores all other costs that user impose on transport systems—road damage, in particular. With this restriction, marginal-cost road pricing would require users to pay only tolls[6] equal to the costs they impose on all other users by adding to congestion levels.

If charged, marginal-cost tolls would play the same role in financing road investments, as do the components of short-run marginal-cost prices that reward private business firms for providing the durable capital equipment they use to produce the commodities they sell. These "productivity rents" dominate the process by which competitive markets reach long-run equilibrium. If the rents a competitive firm earns on its capital equipment exceed the costs of providing that equipment, the firm and, probably, its competitors have an incentive to expand their capacity. So, too, with road authorities. If the productivity rents embodied in a road's congestion tolls exceed the costs of providing the road, expanding it would generate net benefits.

3.2.1 The Basics of Road Improvement Benefit Estimation

A demand schedule for a highway's services tabulates the number of units of the service users purchase at alternative "full prices". By "full price," we mean toll payments plus such directly incurred user costs as those of vehicle operation and the value of the time required for road use.

A variety of demand schedules can be constructed for any given road user. Which of them is relevant for an analysis depends both on the time period and on the nature of the road-service product being studied. In the very short run, shippers and carriers have few degrees of freedom in responding to transportation network changes; delivery schedules and routings can be changed, but origins and destinations are fixed. In a somewhat longer run, truck-fleet characteristics can be changed while, in a still longer run, the number, sizes and locations of factories and warehouses can all be changed.

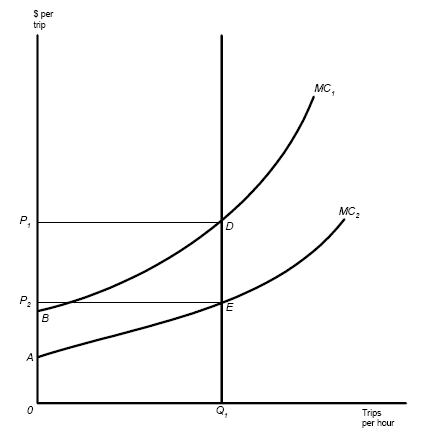
Exhibit 6: Direct very short run benefits of road improvements with marginal-cost tolls.

Suppose that an additional lane in each direction suddenly materializes on the freeway connecting Here and There. On this day, the relevant demand schedule is the vertical line in Exhibit 6. Surprised users discover that congestion has diminished sharply and that, for this reason, the full prices of trips—congestion tolls plus travel times—have fallen fromOP₁ toOP₂. However, too little time has elapsed for them to adjust their travel behavior to take advantage of this change.

As news of the expressway improvement spreads, price and output levels change in a number of related markets. Most obviously, increased speeds and reduced prices on the expressway induce additional use that results in increased congestion and tolls. The increased accessibility the improvement affords may increase the values of neighboring residential, commercial, and industrial sites. The improvement's lower transportation costs apply to goods shipments as well as person trips. As a result, the delivered price of goods produced Here and sold There fall. Faster and, quite likely, more reliable travel may induce cost-saving changes in the production, distribution, and inventory practices of Here and There business firms.

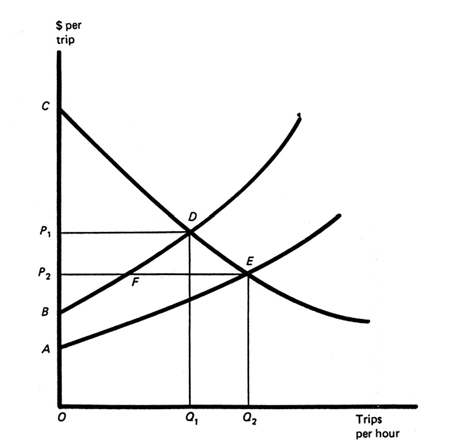
Exhibit 7: Direct intermediate run benefits of road improvements with marginal-cost tolls.

A longer-run equilibrium is pictured at Exhibit 7. On the pre-improvement expressway,OQ₁ trips took place at a price ofOP₁. The net short-run benefit to users derived from these trips can be viewed as the maximum amount users would be willing to pay for them, areaOCDQ₁, minus the tolls they pay and the values of the time and vehicle operating costs they incur in taking them, areaOBDQ₁ yielding a net user benefit of areaCDP₁. In addition, although a cost to consumers, the "quasi-rents,"P₁DB, provided by toll collections are just as much social benefits of road use as are the consumers' surpluses road use generates. The rents are captured by the toll collecting agency, and hence, indirectly, by society at large. Society, in turn, can use these tolls to finance public activities for which taxes would otherwise have to be levied.

The improvement changes net short-run benefits from CDB to CEA per hour. The difference between these two, area BDEA, is the improvement's net benefit. As Exhibit 7 suggests, this net benefit does not, in general, equal its user benefits, the increase in consumers' surplus the improvement generates, areaP₁DEP₂. This user benefit has only area FDE in common with the improvement's net benefit. User benefit equals net benefit only if the remainder of consumer benefit,P₁DFP₂, happens to equal the remainder of net benefit, BFEA. These two magnitudes are equal only if the Here-There road generates the same quasi-rents after the improvement as before it.

In brief, ignoring the improvement's effects on other prices in the economy, its net benefit equals its users' consumers' surplus benefit plus the change in the tolls these users pay. But is it legitimate to ignore the improvement's potential effects on other prices? We believe that it is now generally accepted that changes in land values that road improvements induce are not net benefits of improvements but, rather, that they reflect transfers to land owners of benefits initially received by users. We therefore restrict attention here to effects the Here-There improvement may have on trip costs elsewhere in the highway network and to cost-saving adjustments in production and distribution processes that transport improvements facilitate.

3.2.2 Effects of Improving One Road on Other Roads

To deal in the simplest possible way with the implications of the cost changes that improving one road can induce on other roads, suppose that two rather than one initially identical expressways, Roads 1 and 2, connect Here and There. Travel on these roads has adjusted so that, in equilibrium, each provides the same travel time and congestion tolls. Suddenly an additional lane materializes in each direction on Road 1. As news of this change in travel conditions spreads, Road 2 users shift to Road 1 until, in a new equilibrium, travel times and congestion tolls on the two roads are again equal. Exhibit 8 depicts the old and new longer-run equilibrium.

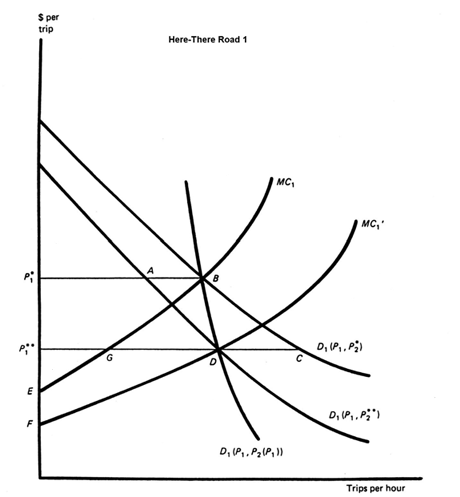
Exhibit 8: Direct and indirect effects of road improvement with marginal cost tolls.

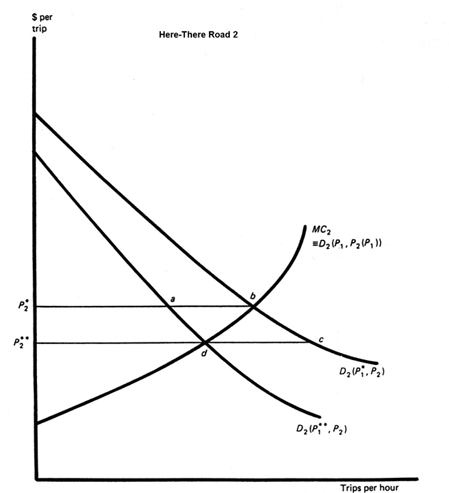
Exhibit 9: Direct and indirect effects of road improvement with marginal cost tolls.

The Here-There expressways provide substitute products. Therefore, any change that reduces the price of trips on Road 1 will divert traffic to it from Road 2. To reflect this interdependence, the demands for trips on Roads 1 and 2 can respectively be writtenD₁(P₁,P₂) andD₂(P₁,P₂) whereP₁ and P₂ refer respectively to the full prices of trips on Roads 1 and 2. Before the improvement, traffic on the two roads is in equilibrium at full prices ofP₁* andP₂*. These are the prices at which "consistent" demand and marginal cost schedules simultaneously intersect on the two roads. In this context, "consistent" intersections involveD₁ (P₁*, P2*) = MC₁ = D₂ (P₁*, P2*) = MC₂. As a result of the improvement in Road 1, its marginal-cost price schedule declines fromMC₁ toMC₁*. This reduction leads both to additional trips by previous Road 1 users and to diversion of trips formerly made on Road 2. Trip diversion reduces the price of trips on Road 2 and hence leads to reverse diversion, i.e., to a shifting to Road 2 of trips formerly made on Road 1. This shifting back and forth ultimately results in a new equilibrium on the two roads at prices ofP₁** andP₂**.

The economics literature suggests several alternative candidates as measures of consumer benefit under conditions such as those depicted in Exhibit 8. The alternative of greatest value in this discussion can be described in the following terms: visualize the price of Road 1 trips as shifting downward, not once and for all, but rather in a long series of tiny steps. Each of these price reductions determines a new, lower equilibrium price of Road 2 trips. That is, the price of Road 2 trips can be viewed as a function,P₂ (P₁), of the price of Road 1 trips. Using this function the price shifts downward, not once and for all but rather in a long series of tiny steps. Each of these price reductions determines a new, lower equilibrium price of Road 2 trips. That is, the price of Road 2 trips can be viewed as a function,P₂ (P₁), of the price of Road 1 trips. Using this function to replace P₂ in both demand schedules results in lines like BD and bd in Exhibits 8 and 9. The line bd "demand schedule," for Road 2 trips, note, is superimposed on that road's marginal cost schedule.

With these two demand schedules, areaP₁*BDP₁** in Exhibit 8 is the improvement's benefit to Road 1 users, whileP₂*bdP₂** is the indirect benefit to Road 2 travelers. At the same time, however,P₂*bdP₂** is also the amount by which quasi-rents (i.e., toll collections) on Road 2 decline as a result of traffic diversion to Road 1. WhileP₂* bdP₂** is, indeed, a benefit to these travelers, this benefit is a transfer to them of income that was formerly collected by society at large as toll revenues. This benefit is, therefore, not a net gain to society that should be added to that on Road 1.[7]

To compare the geometry of Exhibit 8 to that of Exhibit 7, the sum of areasP₁* BD P₁** andP₂*bdP₂** in the more complicated situation is the equivalent ofP₁DEP₂ in the simpler situation. Of the total consumer benefit,P₁DFP₂ in Exhibit 2, andP₁* BG P₁**plus P₂* bd P₂** in Exhibit 8 is the result of a transfer to road users of benefits formerly received by society at large in the form of toll revenues. The basic net short run benefit of the Exhibit 8 improvements is area EBDF, the equivalent of BDEA in Exhibit 7.

To summarize, if marginal cost tolls are charged for trips, determining the net short run benefits of improving a highway link requires only data on the use made of that link. This equals the sum of the change in consumers' surplus and toll revenues on the improved link. The benefit is true even if the improvement affects traffic conditions on other links in the system. Given marginal-cost pricing, changes in consumer benefits and toll revenues on unaltered links would exactly offset each other.

The next two sections elaborate on previous work carried out to describe the nature and extent of re-organization effects. Discussion of marginal cost pricing continues at Section 3.3.

3.2.3 "Industrial Reorganization" Benefits[8]

The ability of a firm to exploit manufacturing scale economies can be limited by the cost of transporting its products to market. A reduction in unit transportation costs can, therefore, yield two types of benefits. First, it provides "direct" benefits by reducing the costs of distributing the outputs of existing manufacturing facilities. Second, a transport cost reduction can makes it efficient to expand the outputs and marketing areas of individual production facilities, thereby taking greater advantage of manufacturing scale economies. This use of more transportation-intensive means of production and distribution in response to reduced transportation costs generates "reorganization" benefits.

This twofold impact of transportation improvements has long been recognized. Consider, for example:

The division of labor…must always be limited…by the extent of the market. When the market is very small, no person can have any encouragement to dedicate himself entirely to one employment…. [B]y means of water carriage a more extensive market is opened to every sort of industry than what land carriage alone can afford it… A broad-wheeled wagon, attended by two men, and drawn by eight horses, in about six weeks time carries and brings back between London and Edinburgh near four ton weight of goods. In about the same time, a ship navigated by six or eight good men, and sailing between the ports of London and Leith, frequently carries and brings back two hundred ton weight of goods….Were there no other communication between these two places, therefore but by land carriage,…they could carry on but a small part of that commerce which at present subsists between them, and consequently give but a small part of that encouragement which they at present mutually afford to each other's industry (Smith [4], pp. 17-19).

Do the analytical frameworks for dealing with transportation improvements that we have dealt with so far in this chapter take into account these "industrial reorganization" benefits of which Adam Smith wrote?[9] Or does adequately accounting for them require the development of special benefit measurement techniques? To see why the answers to these questions are respectively "yes" and "no," it is useful to consider Consolidated Gizmo of America (CGA) which monopolizes American gizmo production, a commodity it distributes over a wide geographical area. Government regulations require that whatever delivered price it sets must be charged all customers, regardless of transportation costs. At the price charged by CGA, g gizmos are demanded yearly in each square mile of its market. Total annual output is gA =G₀ gizmos where A is the area of CGA's entire market.

Inputs to gizmo production are available at prices that are independent of the locations and outputs of individual gizmo factories. Gizmo manufacturing entails increasing returns—a doubling of manufacturing inputs at an individual factory would more than double outputs. The output of a given plant can be expanded, however, only by increasing the plant's market area and, hence, the average cost of transporting gizmos to final consumers. Given these assumptions, CGA would minimize total costs by determining the output per plant, say G*, which minimizes average manufacturing plus distribution costs, and then establishingG₀/G* factories[10] distributed evenly through its market area.

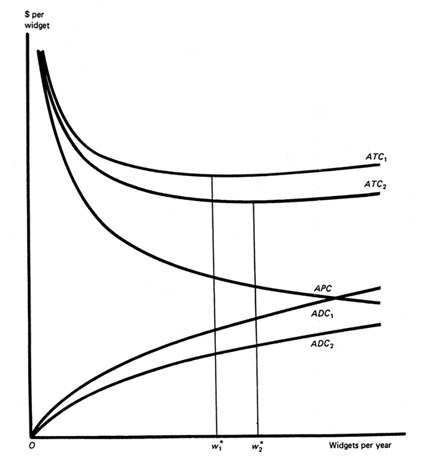
Exhibit 10: Cost characteristics of a single plant.

Exhibit 10 depicts the cost characteristics of a single plant. CurvesADC₁, APC, andATC₁ refer respectively to average distribution, average production, and average total costs before a transportation improvement is made. As the Exhibit is drawn, average total costs first decline with increases in output. In this range, the increase in unit transportation costs as output increases is more than offset by the decrease in unit manufacturing costs. Beyond outputG₁*, however, declines in unit manufacturing costs as output increases are less than sufficient to offset increases in unit transportation costs.

The size of the output level that minimizes an individual factory's sum of unit production and distribution costs depends on several factors. Of particular importance are the geographical density of demand for the product, the magnitude of scale economies, and the level of transportation costs. Actually, it is conceivable that no point such asG₁* would exist. With substantial scale economies and small unit transportation costs, the average-total-cost curve might well decline over a range of outputs so great that a single plant would minimize CGA's total production and distribution costs for its entire marketing area. Under such circumstances, a transportation improvement would not lead CGA to increase its use of transportation services. It would only benefit from reduced costs of the transportation it already uses. Measuring this benefit is straightforward. We therefore restrict attention here to cases in which minimizing total production and distribution costs require several factories.

A reduction in unit transportation costs would immediately lower the costs of distributing gizmos from a group of factories each producing at a rate ofG₁*. In addition, it would make efficient what can be termed a more "transportation-intensive" means of producing and distributing the product. Suppose, to be specific, that a transportation network improvement reduces the average distribution and hence the average total costs of a factory toADC₂ andATC₂ respectively. With such a total-cost reduction, an individual plant's cost-minimizing output would increase fromG₁* toG₂* in Exhibit 4. If the demand for gizmos is fixed, this increased optimum plant size can be realized only by eliminating some factories and, at the same time, relocating and expanding others. This being the case, depicting the aggregate benefits to CGA of a transportation improvement can best be accomplished with a second type of diagram.

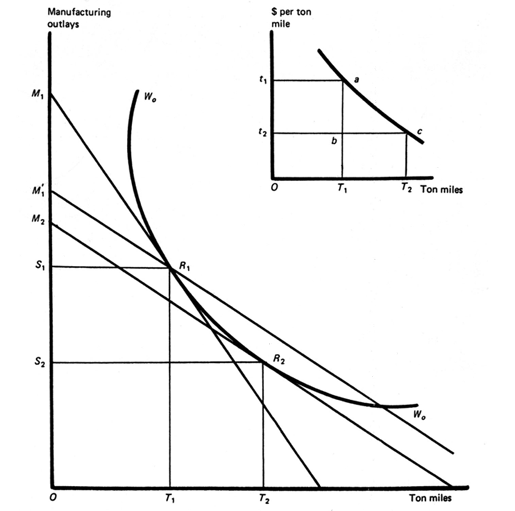
Exhibit 11: Cost minimization choice of transportation and manufacturing outlays.

Alternative manufacturing outlays for CGA's given total output are plotted vertically in Exhibit 11. Again, the level of these costs depends on the sizes of CGA's individual factories. The larger the size (and hence the smaller the number) of individual plants, the lower CGA's total manufacturing costs will be. Factory sizes can be increased, however, only by increasing their marketing areas and, hence, aggregate distribution costs. Transportation inputs measured in some homogeneous unit—e.g. ton miles, product miles, deliveries of average length—are plotted horizontally in this Exhibit.

In Exhibit 11, the lineG₀G₀ is a transportation-input/manufacturing-cost "isoquant." It shows the alternative combinations of transportation inputs and outlays on manufacturing inputs that CGA would require to produce and distributeG₀ gizmos to all of firm's customers. ThatG₀G₀ is drawn with the curvature shown in Exhibit 11a reflects two assumptions about the production-distribution relationship implicit in Exhibit 10. First, scale economies attenuate as plant sizes increase; more exactly, successive equal increases in output produce successively smaller reductions in average production costs. Second, the units of transportation required to distribute an additional unit of output increase as output at each plant increases.

Suppose that the price (if CGA uses common or contract carriers for distribution) or the cost (if it provides its own distribution services) of transportation services is initiallyt₁ dollars per gizmo mile, an amount that is independent of both the length and the size of shipments. The straight lineM₁R₁ (drawn with a slope of−t₁) in Exhibit 11 then represents alternative combinations of production and transportation inputs that can be bought forOM₁ dollars. SinceM₁R₁ is tangent toG₀G₀ atR₁,OM₁ is the minimum cost of manufacturing and distributingG₀ gizmos. AtR₁, CGA spendsOS₁ andOT₁ = S₁M₁ respectively on manufacturing and transportation inputs.

Suppose that improvements are made to the transportation system that reduces the cost of producing ton miles fromt₁ tot₂. If CGA provides its own transportation services, it will receive this benefit directly; if it relies on common or contract carriers and if the transportation industry is competitively organized, it will ultimately receive this benefit through reduced rates. In either event, since a lower outlay is required to purchase a ton mile of transportation services, new and flatter expenditure lines of the sort depicted byM ₁′R₁ andM₂R₂ become relevant. The former expenditure line shows the benefit to CGA if it continues to produce at pointR₁ in Exhibit 11. At that combination of manufacturing and transportation inputs, the transportation improvement affects CGA only by reducing the cost ofOT₁ ton miles fromS₁M₁ toS₁M₁′. This saving can be termed the "direct benefit": the reduced cost of pre-improvement transportation-input purchases.

CGA can derive an additional benefit from the improvement. Undertaking the consolidation of production facilities implied by a move toR₂ in Exhibit 11 would entail increasing transportation purchases fromOT₁ toOT₂ gizmo miles and increasing total outlays on transportation fromS₁M₁′ toS₂M₂. This increase in transportation outlays would be more than offset by the associated reduction ofS₁S₂ in the cost of the manufacturing inputs required to produce and distributeG₀ gizmos. Specifically, the shift fromR₁ toR₂ would result in an additional savings ofM₁′M₂ in total costs. This latter saving is the "reorganization benefit" of the improvement: the cost reduction achievable by substituting transportation for manufacturing inputs. Exhibit 11b depicts CGA's demand schedule for transportation associated with the shift fromR₁ toR₂. In this diagram, the areat₁abt₂ is the direct benefit—the reduction in the cost ofOT₁ gizmo miles brought about by the reduction in their price fromt₁ tot₂. This area is equal toM₁M₁′ in Exhibit 11a, while area abc is equal to M₁′M₂, the reorganization benefit.

We should emphasize that the preceding analysis can easily be adapted to deal with a wide variety of benefit-measurement situations. With suitable re-labeling, Exhibit 10 and Exhibit 11 can be used to deal with the utility-maximizing allocation of a consumer's budget between one commodity and all others available to him, or to discuss the choices faced by a producer in selecting the cost minimizing quantities of any inputs used in its production and distribution process. Had "input T" been substituted for "gizmo miles" or "transportation services" in the above discussion, the conclusions reached would not have changed. A consumer's surplus-type measure of transportation improvement benefits would be accurate under precisely the same circumstances as would such a measure of the benefits of any other cost reduction.

3.2.4 A Sample Benefit Estimation Model

Since the reorganization benefits of transport improvements are both important and difficult to measure, estimating the relative sizes of direct and reorganization benefits could be of value even for so simple a model as the following:

1. Consolidated Gizmo's manufacturing process is homogeneous of order1/a. That is, increasing each one of its factory's inputs by the same positive fraction, k, results in output increasing by a factor ofk^1/a. If the prices of these inputs are independent of both the factory's location and the quantities in which it buys, it is possible to show that the cost of manufacturing G gizmos at a factory can be written
   
   M(G ) = f G ^a
   
   where the coefficient, f, is a function of input prices the form of which depends on the gizmo production function's characteristics.

2. The cost of a gizmo-mile of road services is t regardless of both length of haul and shipment size. Transportation can take place only north-south or east-west on a dense rectangular grid of roads. (This assumption greatly simplifies algebra. It allows working with a square market area for which any point on the boundary is the same distance from the factory.)
3. CGA must charge all gizmo buyers the same price regardless of how far they live from the factory that serves them. At this price, g gizmos a year are sold in each square mile of CGA's market area.

Given these assumptions, very tedious algebra[11] leads to the following conclusions: The total cost of delivering the G gizmos a factory produces is

T(G) = (2/g)^½ t G^3/2/3

The average cost of manufacturing and delivering the output for a factory and, hence, for the firm as a whole, is

C(G) = f G ^a−1 + (2G/g)^½ t /2

The factory's cost-minimizing output is

G* = [3(1 − a) f (2g)^½/t]b

whereb = 2/(3 − a). Substituting the expression for G* into the expressions for transportation and manufacturing costs would yield expressions for minimum total production and distribution costs. However, useful and appreciably simpler expressions can be obtained from a finding that the ratios of average total to average manufacturing costs and average distribution to average manufacturing costs can respectively be written,

C(G*)/[f (G*)^a−1] = 3 − 2a

[T(G*)/G*]/[f G* ^a−1] = 2(1 − a)

Holding the output of all of CGA's factories fixed at gA where A is the firm's entire market area, its demand for transportation services is

D(T |gA) = 2(1 − a) g A B[^{(3/2−a)/(1−a)}] (f/t)^1/[2(1−a)]

WhereB = 3(1 − a)(2g)^½. The total benefit of a decline in the price of a product-mile of transport from, say, t to et turns out to be

Ben = (3 − 2a) g A (t/B)^{[(3/2−a)/(1−a)]} f ^1/[2(1−a)] [1− e^{[(3/2−a)/(1−a)]}]

DividingD(T |gA) by Ben yields this expression:

(direct benefits)/(total benefits) = 2 (1 − e) (1 − a)/[(3 − 2a)(1 − e^{[(3/2−a)/(1−a)]})]

For a 25% reduction in the price of a product-mile of transport, Table 2 gives values of this and related expressions for alternative values of a, the scale-economies index. The results are, in a way, disappointing. Even for the smallest scale-economies index value considered, e = 0.95, reorganization benefits account for only 12% of total benefits.

Table 2: Cost Ratios and Benefits of a 25% Reduction in Transport Prices

Manufacturing Scale Economies Index Reduction in t	Ratio of Distribution to Total Costs	Total Cost Reduction from 25%	Ratio of Direct to Total Costs
a	(3/2−a)/(1−a)	1 − 0.75(1−a)/(3/2−a)	Ben
0.95	9.1%	2.6%	88.1%
0.90	16.7%	4.7%	89.0%
0.85	23.1%	6.4%	89.7%
0.80	28.6%	7.9%	90.5%
0.75	33.3%	9.1%	91.2%
0.70	37.5%	10.2%	91.6%
0.65	41.2%	11.2%	92.2%
0.60	44.4%	12.0%	92.6%
0.55	47.4%	12.7%	93.0%
0.50	50.0%	13.5%	93.3%

But much more can be said. When we write about the costs people incur in traveling, we almost always include the values they attach to the time their trips require. Recently, work of Ken Small and others [8] has established that costs related to the variability of travel time are also very important. In talking of goods movement, however, we usually still write as if the dollars shippers pay carriers for moving, e.g., ton miles of gizmos cover the entire costs of shipments. Not so. Shipment time and its variability matter just as much to shippers as travel-time and its variability matter to people.

What are the time and time-variability costs of shipments? Back in the good old days of the ICC, a plywood manufacturer in Oregon could, in the late fall or winter, load a boxcar with its product and send it to Boston, say. Its right to specify the shipment's routing enabled it to maximize the number of rail yards through which it passed. When, after a month or two or three, a customer was found for the plywood, the shipper would change the destination and routing of its mobile warehouse and send it as rapidly as possible to Cleveland, say.

Now, much more normal are situations in which an increase in travel time and its variability is costly. Most obviously, money tied up in inventory isn't earning interest. The longer it takes to ship perishable goods (e.g., fresh fruit and vegetables, newspapers and magazines, high fashion clothing), the more they depreciate. It's the near elimination of travel-time variability that makes possible the "just-in-time" inventory management that has come to dominate automotive and other complex assembly processes.

The simple model that underlies Table 2 completely ignores these time-related costs of transportation. Taking them into account might well result in reorganization benefits that are an order of magnitude or more greater than those suggested by Table 2.

previous | next