Effectiveness of Safety and Public Service Announcement Messages on Dynamic Message Signs
Appendix B: Sample Size Calculation
Observational studies such as the one in this task order differ from controlled studies, and any statistical models developed need to include potential covariates and interaction effects. The greater the number of covariates, the greater the sample size needed to ensure sufficient power to minimize Type II errors. There is a need to be sufficiently confident that any insignificant findings observed are not due to large variations in too small a sample and that any impacts from outliers are minimized.
In the absence of subject compensation, and based on past studies, a 25- to 30-percent survey response rate is anticipated.
Simple random sampling is used to compute the needed sample size. The necessary sample size is calculated such that:
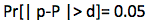 Equation 1
Equation 1
Where:
- p is the estimated proportion of people who will engage in a certain behavior (for example, wear seat belt)
- P is the true proportion of people in the target population that will engage in a certain behavior
- d is the margin of error—it specifies the desired level of precision in the sample estimate, p, to be with respect to P.
Equation 1 above states that the sample size is calculated such that there is only 5-percent chance (or with a 95-percent confidence level) that the sample estimate p will deviate from the true population parameter P by more than d. Derived from equation 1, the formula to calculate the number of survey responses needed n becomes:
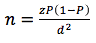 Equation 2
Equation 2
Where:
- z is equal to 1.96 at a 95-percent confidence level
To calculate n, both p and d need to be specified and n varies as p and d change. The larger the sample size, the smaller is the margin of error. P (See Table 32 for examples) will be estimated from the pilot survey (it can also be obtained from the existing literature, i.e., based on experience).
Table 32. Needed number of responses n as a function of P and d.
| d\P |
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
| 0.05 |
71 |
125 |
165 |
188 |
384 |
| 0.075 |
31 |
56 |
73 |
84 |
87 |
| 0.1 |
18 |
31 |
41 |
47 |
49 |
| 0.15 |
8 |
14 |
18 |
21 |
22 |
n refers to the number of responses. Thus, assuming a 10-percent response rate, the final sample size needed should be 10*n.
If the sample estimate p is 0.5 and the margin of error is d is 0.05, then a sample size of N=384
is reasonable.
It is important to note that this is the number of surveys that need to be returned and not the number distributed, which will need to be much higher. The response rates for each survey conducted in past studies have varied (from 10 percent to 35 percent), which creates sampling biases that also need to be accounted for statistically.
Given these estimates, 500 surveys need to be returned per site. Thus, with four sites,
2000 total surveys should be sufficient to achieve a 95-percent confidence interval.