2. Methodology for Measuring Regional Reorganization Effects

2.1 Development of Regional Subgroups

The development of a regional analysis focused on applying the analytical framework developed for the national analysis to geographically grouped sets of corridors. A primary task of the regional analysis has been the development of regional groups to analyze the reorganization effects related to highway freight improvements. The project team developed three proposed regional groupings: A five-region model, a three-region model based on FHWA's Federal Lands Program (FLP) regions, and a distributed three-region model.

These regional models were then applied to the corridors used in the Phase II national analysis and a determination was made of the number of corridors available within each model for each proposed region. Table 3 lists the corridors used in the national analysis conducted under Phase II.

Table 3. Corridors Used in National Analysis

Corridor	Code
Atlanta-Jacksonville	ATL-JAX
Atlanta-Knoxville	ATL-KNX
Atlanta-Mobile	ATL-MOB
Birmingham-Chattanooga	BIR-CHA
Birmingham-Nashville	BGH-NSH
Cleveland-Columbus	CLE-COL
Columbus-Pittsburgh	PIT-COL
Dallas-Houston	DAL-HOU
Dayton-Detroit	DAY-DET
Harrisburg-Philadelphia	HAR-PHI
Indianapolis-Chicago	IND-CHI
Indianapolis-Columbus OH	IND-COL
Kansas City-St Louis	KNC-STL
Knoxville-Dayton	KNX-DAY
Louisville-Columbus	COL-LOU
Louisville-Indianapolis	IND-LOU
Mobile-New Orleans	MOB-NOR
Nashville-Louisville	NSH-LOU
Nashville-St Louis	NSH-STL
New Orleans-Birmingham	NOR-BIR
Richmond-Philadelphia	RIC-PHI
San Antonio-Houston	SAN-HOU
St Louis-Indianapolis	STL-IND
Denver-Kansas City	DEN-KAN
Denver-Salt Lake City	DEN-SAL
San Francisco-Salt Lake City	SFO-SAL
San Francisco-Los Angeles	SFO-LAX
Portland-Seattle	POR-SEA
Boston-New York City	NYC-BOS
Harrisburg-New York City	NYC-HAR

This original set of corridors represented a selection of freight-significant corridors of varying lengths, traffic volumes, and performance characteristics. However, the corridors are concentrated in the Midwest and lack good representation for some parts of the country. This problem was addressed by adding new corridors to the analysis, as discussed later.

Table 4 describes the division of the corridors originally used in the national analysis into the proposed five regions.

Table 4. Original Corridors Incorporated into Five Regions

Region	Corridor	Code
East Coast	Harrisburg-Philadelphia	HAR-PHI
	Richmond-Philadelphia	RIC-PHI
	Boston-New York City	NYC-BOS
	Harrisburg-New York City	NYC-HAR
Southeast	Atlanta-Jacksonville	ATL-JAX
	Atlanta-Knoxville	ATL-KNX
	Atlanta-Mobile	ATL-MOB
	Birmingham-Chattanooga	BIR-CHA
	Birmingham-Nashville	BGH-NSH
	Mobile-New Orleans	MOB-NOR
	New Orleans-Birmingham	NOR-BIR
Midwest	Cleveland-Columbus	CLE-COL
	Columbus-Pittsburgh	PIT-COL
	Dayton-Detroit	DAY-DET
	Indianapolis-Chicago	IND-CHI
	Indianapolis-Columbus OH	IND-COL
	Kansas City-St Louis	KNC-STL
	Knoxville-Dayton	KNX-DAY
	Louisville-Columbus	COL-LOU
	Louisville-Indianapolis	IND-LOU
	Nashville-Louisville	NSH-LOU
	Nashville-St Louis	NSH-STL
	St Louis-Indianapolis	STL-IND
Southwest	Dallas-Houston	DAL-HOU
	San Antonio-Houston	SAN-HOU
West Coast	Denver-Kansas City	DEN-KAN
	Denver-Salt Lake City	DEN-SAL
	San Francisco-Salt Lake City	SFO-SAL
	San Francisco-Los Angeles	SFO-LAX
	Portland-Seattle	POR-SEA

The five-region model allows for an easily understandable allocation of corridors to regions with which most practitioners would recognize and identify. However, it creates problems of under-representation, particularly in the Southwest and East. Using a five-region model would require significant investment in collecting data for a sufficient number of corridors to cover each region.

Table 5 describes the division of the corridors originally used in the national analysis into the proposed three FHWA FLP regions.

Table 5. Original Corridors Incorporated into FHWA's Federal Lands Program Regions

Region	Corridor	Code
Eastern Region	Atlanta-Jacksonville	ATL-JAX
	Atlanta-Knoxville	ATL-KNX
	Atlanta-Mobile	ATL-MOB
	Birmingham-Chattanooga	BIR-CHA
	Birmingham-Nashville	BGH-NSH
	Cleveland-Columbus	CLE-COL
	Columbus-Pittsburgh	PIT-COL
	Dayton-Detroit	DAY-DET
	Harrisburg-Philadelphia	HAR-PHI
	Indianapolis-Chicago	IND-CHI
	Indianapolis-Columbus OH	IND-COL
	Kansas City-St Louis	KNC-STL
	Knoxville-Dayton	KNX-DAY
	Louisville-Columbus	COL-LOU
	Louisville-Indianapolis	IND-LOU
	Mobile-New Orleans	MOB-NOR
	Nashville-Louisville	NSH-LOU
	Nashville-St Louis	NSH-STL
	New Orleans-Birmingham	NOR-BIR
	Richmond-Philadelphia	RIC-PHI
	Boston-New York City	NYC-BOS
	Harrisburg-New York City	NYC-HAR
	St Louis-Indianapolis	STL-IND
Central Region	Dallas-Houston	DAL-HOU
	Denver-Kansas City	DEN-KAN
	Denver-Salt Lake City	DEN-SAL
	San Francisco-Salt Lake City	SFO-SAL
	San Francisco-Los Angeles	SFO-LAX
	San Antonio-Houston	SAN-HOU

Using FHWA's FLP regions as the model for sub-national division creates significant concentration in the East. In addition, the West region becomes extremely small, with only one corridor allocated.

Table 6 describes the division of the corridors originally used in the national analysis into the proposed three distributed regions.

Table 6. Original Corridors Incorporated into Three Regions

Region	Corridor	Code
East Coast	Atlanta-Jacksonville	ATL-JAX
	Atlanta-Knoxville	ATL-KNX
	Atlanta-Mobile	ATL-MOB
	Birmingham-Chattanooga	BIR-CHA
	Birmingham-Nashville	BGH-NSH
	Harrisburg-Philadelphia	HAR-PHI
	Mobile-New Orleans	MOB-NOR
	New Orleans-Birmingham	NOR-BIR
	Richmond-Philadelphia	RIC-PHI
	Boston-New York City	NYC-BOS
	Harrisburg-New York City	NYC-HAR
Midwest	Cleveland-Columbus	CLE-COL
	Columbus-Pittsburgh	PIT-COL
	Dayton-Detroit	DAY-DET
	Indianapolis-Chicago	IND-CHI
	Indianapolis-Columbus OH	IND-COL
	Kansas City-St Louis	KNC-STL
	Knoxville-Dayton	KNX-DAY
	Louisville-Columbus	COL-LOU
	Louisville-Indianapolis	IND-LOU
	Nashville-Louisville	NSH-LOU
	Nashville-St Louis	NSH-STL
	St Louis-Indianapolis	STL-IND
West Coast	Dallas-Houston	DAL-HOU
	San Antonio-Houston	SAN-HOU
	Denver-Kansas City	DEN-KAN
	Denver-Salt Lake City	DEN-SAL
	San Francisco-Salt Lake City	SFO-SAL
	San Francisco-Los Angeles	SFO-LAX

The distributed three-region model reduces the potential variability between regions that would be in a five-region model. It creates regional allocations with which practitioners can identify, but the three-region model reduces the burden of additional data collection to achievable proportions.

The three proposed regional division models are:

Five-Region Model

Regions	Corridors
Midwest	12
East Coast	4
Southeast	7
Southwest	2
West Coast	5

Three-Region FLP Model

Regions	Corridors
Central	6
Eastern	23
Western	1

Three-Region Model

Regions	Corridors
Midwest	12
East Coast	11
West Coast	7

The three-region FLP model was determined as untenable due to the heavy weighting of states included in the Eastern region and the lack of good mapping to freight-significant corridors with the southern half of the West Coast included in the Central region and most of the Midwest included in the Eastern region. As can be seen from the table above, the FLP approach allowed only one of the original corridors to be included in the third (Western) region.

2.2 Testing of Regional Subgroups

The project team tested a selection of the subgroups for performance using the three final equations developed under Phase II: The pooled regression equation, the regression with fixed effects, and the general least squares regression with fixed effects. The objectives of the testing were:

• To estimate the likely minimum number of corridors or observations required per region in order to derive significant results;
• To determine the data collection required in order to develop a robust regional dataset; and
• To use this information to determine which regional definition to use in the final analysis.

In order to estimate the likely minimum number of corridors or observations required, each of the three equations developed for the Phase II national analysis were re-run using the midwestern corridors from the five-region model and the East Coast corridors from the three-region model. In addition, the 23-corridor FLP Eastern region was included in order to improve the estimate of the required minimum number of corridors or observations required. However, as discussed earlier, the FLP model was determined unsuitable for use as a final regional grouping.

Equation 1: Pooled Regression

Equation 1 uses a semi-log functional form with data on freight demand, congestion related delays, and economic variables. In the following model, demand for daily truck traffic is specified as a function of per capita income, GDP growth rate, LTL rates, and delay. Table 7 provides the results from the original national analysis.

Estimating Equation:LOG(Trucks/day_r,t) = β₀ + β₁ * Delay_r,t + β₂ * GDP Growth_r,t + β₃ Real per Capita Income_r,t + β4 * LTL Rate_r,t

Table 7. Regression Results for Freight Demand (Pooled Regression)

Variable	Coefficient	Std. Error	t-Statistic	Probability of Non-Significance
Constant	8.162777	0.061204	133.3699	0.0000
Delay	-0.001834	0.000418	-4.388016	0.0000
GDP Growth	0.067249	0.010604	6.342005	0.0000
Real per Capita Income	6.16E-05	4.67E-06	13.19443	0.0000
Real LTL Rates	-0.004517	0.000296	-15.26863	0.0000
R-squared	0.323195	Mean dependent variable		8.805702
Adjusted R-squared	0.308871	S.D. dependent variable		0.389423
S.E. of regression	0.323743	Sum squared residual		19.80905
Durbin-Watson stat	0.142865

Method: GLS (Cross-Section Weights)
Total panel (unbalanced) observations: 194

Where:

• Trucks/day = Average number of trucks/day for the corridor
• Delay = Average delay per mile
• GDP Growth = Growth rate for the Gross Domestic Product
• Real Per Capita Income = Average Per Capita income for all counties along the corridors
• LTL Rates/trip = Less-than-truckload rates for 1,000 lb. shipment

For the national analysis, this specification produced coefficients that are of the expected sign. Further estimation also suggested that the coefficient of the delay variable may vary across corridors of various lengths and be higher in absolute terms for long routes (over 400 miles) than for short routes (up to 200 miles) and medium routes (200 to 400 miles). However, the Durbin-Watson (DW) statistic in the above specification was low, at around 0.14. A low DW statistic indicates a potential problem of autocorrelation within and across the individual cross-sections (or other forms of misspecification). This arises from complications with panel data, in particular:

• Errors are not independent between time periods and
• Errors are correlated between corridors.

As such, re-estimating Equation 1 with fewer observations was not expected to produce strong results. Table 8 describes the results of Equation 1 for each of the three regional sub-groups tested.

Table 8. Results for Equation 1 for Three Regional Sub-groups (FHWA Eastern Region)

Three-Region FLP Model FHWA Eastern Region 23 corridors with 2 no-data corridors 21 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 21
Total pool (unbalanced) observations: 151
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.245	0.127	64.774	0.000
Delay	0.001	0.002	0.243	0.809
GDP Growth	0.040	0.026	1.524	0.130
Real Per Capita Income	0.000	0.000	5.109	0.000
Real LTL Rates	-0.001	0.000	-2.455	0.015
R-squared	0.999	Mean dependent var		13.772
Adjusted R-squared	0.999	S.D. dependent var		7.762
S.E. of regression	0.234	Sum squared resid		7.966
Durbin-Watson stat	0.318

Table 8. Results for Equation 1 for Three Regional Sub-groups (East combined)

Three-Region Model East (combined) 11 corridors with 2 no-data corridors 9 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 9
Total pool (unbalanced) observations: 65
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	7.873	0.166	47.487	0.000
Delay	-0.006	0.001	-3.874	0.000
GDP Growth	0.039	0.042	0.919	0.362
Real Per Capita Income	0.000	0.000	6.268	0.000
Real LTL Rates	-0.002	0.001	-2.147	0.036
R-squared	0.994	Mean dependent var		10.448
Adjusted R-squared	0.994	S.D. dependent var		2.972
S.E. of regression	0.232	Sum squared resid		3.241
Durbin-Watson stat	0.265

Table 8. Results for Equation 1 for Three Regional Sub-groups (Midwest)

Three-Region Model Midwest 12 corridors with 0 no-data corridors 12 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 12
Total pool (unbalanced) observations: 86
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.604	0.149	57.930	0.000
Delay	0.004	0.003	1.568	0.121
GDP Growth	0.037	0.030	1.258	0.212
Real Per Capita Income	0.000	0.000	1.920	0.058
Real LTL Rates	-0.001	0.001	-1.028	0.037
R-squared	0.999	Mean dependent var		13.183
Adjusted R-squared	0.999	S.D. dependent var		5.737
S.E. of regression	0.192	Sum squared resid		2.990
Durbin-Watson stat	0.390

As expected, each of the regional subgroups performed poorly in terms of the DW statistic, ranging from.0.29 to 0.36. None of the equations achieved significant results for all included variables. The 65-observation Eastern region achieved significant and correctly signed results for the Delay variable, which is the key measure of highway performance included in the equation.

Equation 2: Regression with Fixed Effects

To mitigate the problems associated with Equation 1, the model was re-estimated using the fixed effects method during the Phase II national analysis. The estimating equation was reformulated as

Estimating Equation:LOG(Trucks/day_r,t) = β_r + β₁ * Delay_r,t + β₂ * GDP Growth_r,t

Whereβ_{r ( r = 1…28)} are corridor-specific constant, or fixed effects.

The results of the estimation developed for the national analysis are provided in Table 9.

Table 9. Regression Results for Freight Demand (Fixed Effects)

Variable	Coefficient	Std. Error	t-Statistic	Probability of Non-Significance
Delay	-0.002575	0.000496	-5.186827	0.0000
GDP Growth	0.073356	0.007632	9.611514	0.0000
Fixed Effects
Atlanta-Jacksonville	8.716456
Atlanta-Knoxville	8.918446
Atlanta-Mobile	8.362351
Birmingham-Nashville	8.353916
Cleveland-Columbus	8.605421
Columbus-Pittsburgh	8.535460
Dallas-Houston	8.623438
Dayton-Detroit	8.592172
Harrisburg-Philadelphia	8.526888
Indianapolis-Chicago	8.655297
Indianapolis-Columbus	8.821301
Kansas City-St. Louis	8.610851
Knoxville-Dayton	8.807753
Louisville-Columbus	8.708366
Louisville-Indianapolis	8.679238
Mobile-New Orleans	8.325837
Nashville-Louisville	9.049711
Nashville-St. Louis	8.086613
Richmond-Philadelphia	9.035896
San Antonio-Houston	8.423007
St. Louis-Indianapolis	8.664829
Denver-Kansas City	7.441348
Denver-Salt Lake City	8.156259
San Francisco-Salt Lake City	7.459972
San Francisco-Los Angeles	8.343404
Portland-Seattle	8.794208
Boston-New York City	8.639654
Harrisburg-New York City	8.727643
R-squared	0.924207	Mean dependent variable		8.805702
Adjusted R-squared	0.910804	S.D. dependent variable		0.389423
S.E. of regression	0.116304	Sum squared residual		2.218348
Durbin-Watson stat	1.117309

Method: GLS (Cross-Section Weights)
Total panel (unbalanced) observations: 194

For the national analysis, the high R-squared value, 0.92 indicated that the variables considered explain changes in freight demand very closely. Delay and GDP growth variables have the correct signs, and they are statistically significant. The DW statistic, 1.11, is significantly higher than that reported in the first model.

Equation 2 was also re-run using the three regional subgroups. Table 10 describes the results for each.

Table 10. Results for Equation 2 for Three Regional Sub-groups (FHWA Eastern Region)

Three-Region FLP Model FHWA Eastern Region 23 corridors with 2 no-data corridors 21 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 21
Total pool (unbalanced) observations: 151
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.682	0.045	192.020	0.000
Delay	-0.005	0.001	-6.088	0.000
GDP Growth	0.065	0.011	5.685	0.000
Fixed Effects:
ATL-JAX	0.071
ATL-KNX	0.270
ATL-MOB	-0.289
BGH-NSH	-0.297
CLE-COL	-0.037
PIT-COL	-0.115
DAY-DET	-0.055
HAR-PHI	-0.104
IND-CHI	0.007
IND-COL	0.175
KNC-STL	-0.013
KNX-DAY	0.195
COL-LOU	0.063
IND-LOU	0.030
MOB-NOR	-0.320
NSH-LOU	0.425
NSH-STL	-0.564
RIC-PHI	0.397
STL-IND	0.015
NYC-BOS	0.026
NYC-HAR	0.080
R-squared	0.999	Mean dependent var		12.179
Adjusted R-squared	0.999	S.D. dependent var		4.820
S.E. of regression	0.110	Sum squared resid		1.539
Durbin-Watson stat	1.179

Table 10. Results for Equation 2 for Three Regional Sub-groups (East combined)

Three-Region Model East (combined) 11 corridors with 2 no-data corridors 9 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 9
Total pool (unbalanced) observations: 65
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.626	0.058	148.596	0.000
Delay	-0.005	0.001	-5.887	0.000
GDP Growth	0.076	0.015	4.958	0.000
Fixed Effects:
ATL-JAX	0.086
ATL-KNX	0.285
ATL-MOB	-0.274
BGH-NSH	-0.282
HAR-PHI	-0.093
MOB-NOR	-0.305
RIC-PHI	0.412
NYC-BOS	0.041
NYC-HAR	0.091
R-squared	0.999	Mean dependent var		13.535
Adjusted R-squared	0.999	S.D. dependent var		6.478
S.E. of regression	0.137	Sum squared resid		1.009
Durbin-Watson stat	1.176

Table 10. Results for Equation 2 for Three Regional Sub-groups (Midwest)

Three-Region FLP Model Midwest 12 corridors with 0 no-data corridors 12 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 12
Total pool (unbalanced) observations: 86
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.727	0.063	137.923	0.000
Delay	-0.005	0.002	-2.357	0.021
GDP Growth	0.056	0.016	3.534	0.001
Fixed Effects:
CLE-COL	-0.047
PIT-COL	-0.125
DAY-DET	-0.064
IND-CHI	-0.002
IND-COL	0.166
KNC-STL	-0.023
KNX-DAY	0.177
COL-LOU	0.052
IND-LOU	0.022
NSH-LOU	0.410
NSH-STL	-0.574
STL-IND	0.007
R-squared	0.999	Mean dependent var		10.104
Adjusted R-squared	0.999	S.D. dependent var		3.201
S.E. of regression	0.085	Sum squared resid		0.518
Durbin-Watson stat	1.149

As with the national analysis, Equation 2 performed well for each of the regional groupings, all with R-squared statistics above 0.99.

Equation 3: GLS Regression with Fixed Effects

The model was also estimated with V/C ratio and "fixed effects." The estimating equation was reformulated as:

Estimating Equation:LOG(Trucks/day_r,t) = β_r + β₁ * VC Ratio_r,t + β₂ * GDP Growth_r,t β₃ * Real per Capita Income_r,t + β4 * Real LTL Rate_r,t

Whereβ_{r ( r = 1…28)} are corridor-specific constant, or fixed effects.

Table 11 describes the results of the original national analysis using Equation 3.

In the original national analysis, this model had a high R-squared value (0.954), indicating that the selected variables are highly correlated with changes in demand for transportation. The VC Ratio, GDP Growth, and Real Per Capita Income variables have the correct signs. The VC Ratio and Real LTL Rate variables are statistically significant. The DW statistic is higher than earlier estimations.

Table 11. GLS Regression Results for Freight Demand with Cross Section Weights (Fixed Effects)

Variable	Coefficient	Std. Error	t-Statistic	Probability of Non-Significance
VC Ratio	-0.145737	0.024236	-6.013214	0.0000
GDP Growth	0.005716	0.004550	1.256128	0.2109
Real Per Capita Income	8.11E-06	4.04E-06	2.006642	0.0465
Real LTL Rates	0.003148	0.000230	13.65898	0.0000
Fixed Effects
Atlanta-Jacksonville	-0.145737
Atlanta-Knoxville	0.005716
Atlanta-Mobile	8.11E-06
Birmingham-Nashville	0.003148
Cleveland-Columbus
Columbus-Pittsburgh	8.343270
Dallas-Houston	8.671927
Dayton-Detroit	7.985723
Harrisburg-Philadelphia	7.827820
Indianapolis-Chicago	8.331450
Indianapolis-Columbus	8.187617
Kansas City-St. Louis	8.232353
Knoxville-Dayton	8.249458
Louisville-Columbus	8.055459
Louisville-Indianapolis	8.262573
Mobile-New Orleans	8.492228
Nashville-Louisville	8.111981
Nashville-St. Louis	8.373134
Richmond-Philadelphia	8.328012
San Antonio-Houston	8.378806
St. Louis-Indianapolis	8.150193
Denver-Kansas City	8.808472
Denver-Salt Lake City	7.632464
San Francisco-Salt Lake City	8.470470
San Francisco-Los Angeles	8.100525
Portland-Seattle	8.268212
Boston-New York City	6.563344
Harrisburg-New York City	7.438120
R-squared	0.954116	Mean dependent var		8.805702
Adjusted R-squared	0.945336	S.D. dependent variable		0.389423
S.E. of regression	0.091048	Sum squared residual		1.342952
Durbin-Watson stat	1.315943

This model performed well using the entire set of corridors, but sub-division into smaller groupings with fewer observations indicated that the nine- and 12-corridor groupings did not have a sufficient number of observations to generate statistically significant results.

The results of the three regional analyses are described in Table 12.

Table 12. Results for Equation 3 for Three Regional Sub-groups (FHWA Eastern Region)

Three-Region FLP Model FHWA Eastern Region 23 corridors with 2 no-data corridors 21 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 21
Total pool (unbalanced) observations: 151
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.223	0.104	78.752	0.000
VC_Ratio	-0.162	0.037	-4.361	0.000
GDP_Growth	0.003	0.009	0.383	0.703
Real Per Capita Income	0.000	0.000	0.867	0.388
Real LTL Rates	0.003	0.001	4.392	0.000
Fixed Effects:
ATL-JAX	0.095
ATL-KNX	0.426
ATL-MOB	-0.264
BGH-NSH	-0.424
CLE-COL	0.088
PIT-COL	-0.060
DAY-DET	0.001
HAR-PHI	-0.193
IND-CHI	0.008
IND-COL	0.246
KNC-STL	-0.137
KNX-DAY	0.129
COL-LOU	0.081
IND-LOU	0.131
MOB-NOR	-0.088
NSH-LOU	0.567
NSH-STL	-0.620
RIC-PHI	0.217
STL-IND	0.018
NYC-BOS	-0.184
NYC-HAR	-0.201
R-squared	0.999	Mean dependent var		15.836
Adjusted R-squared	0.999	S.D. dependent var		18.020
S.E. of regression	0.090	Sum squared resid		1.020
Durbin-Watson stat	1.1896

Table 12. Results for Equation 3 for Three Regional Sub-groups (East combined)

Three-Region Model East (combined) 11 corridors with 2 no-data corridors 9 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 9
Total pool (unbalanced) observations: 65
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	7.796	0.210	37.165	0.000
VC_Ratio	-0.088	0.072	-1.223	0.227
GDP_Growth	0.000	0.016	-0.027	0.979
Real Per Capita Income	0.000	0.000	1.391	0.170
Real LTL Rates	0.002	0.002	1.219	0.228
Fixed Effects:
ATL-JAX	0.179
ATL-KNX	0.464
ATL-MOB	-0.184
BGH-NSH	-0.251
HAR-PHI	-0.180
MOB-NOR	-0.001
RIC-PHI	0.248
NYC-BOS	-0.214
NYC-HAR	-0.206
R-squared	0.999	Mean dependent var		15.440
Adjusted R-squared	0.999	S.D. dependent var		8.714
S.E. of regression	0.112	Sum squared resid		0.650
Durbin-Watson stat	1.221

Table 12. Results for Equation 3 for Three Regional Sub-groups (Midwest)

Five-Region Model Midwest 12 corridors with 0 no-data corridors 12 corridors for analysis
Dependent Variable: LOG(AADT-Trucks)
Method: Pooled EGLS (Cross-section weights)
Included observations: 8
Cross-sections included: 12
Total pool (unbalanced) observations: 86
Variable	Coef	Std. Error	t-Stat	Prob.
Constant	8.487	0.132	64.309	0.000
VC_Ratio	0.071	0.122	0.581	0.563
GDP_Growth	0.014	0.016	0.841	0.403
Real Per Capita Income	0.000	0.000	-1.430	0.157
Real LTL Rates	0.005	0.001	4.389	0.000
Fixed Effects:
CLE-COL	0.039
PIT-COL	-0.093
DAY-DET	-0.003
IND-CHI	0.118
IND-COL	0.203
KNC-STL	-0.289
KNX-DAY	-0.062
COL-LOU	-0.005
IND-LOU	0.156
NSH-LOU	0.522
NSH-STL	-0.660
STL-IND	-0.006
R-squared	0.999	Mean dependent var		14.241
Adjusted R-squared	0.999	S.D. dependent var		19.442
S.E. of regression	0.070	Sum squared resid		0.341
Durbin-Watson stat	1.311

2.3 Selection of the Regional Groupings

The results of the analysis of the proposed regional groupings indicate that results generating reliability similar to that in the Phase II national analysis require groupings with an estimated minimum of 15–20 corridors. It can not be determined in advance of data collection and re-analysis whether any particular grouping will generate usable results. However, the performance of the test groupings against the three Phase II equations did not demonstrate any particular regional weakness.

Given the need for a regional grouping where every defined region needs at least 15-20 corridors, the project group and FHWA selected the distributed three-region grouping and began the task of collecting data for additional corridors to generate sufficient observations for each region. Having experienced issues related to incomplete data during the Phase II analysis, the project team selected sufficient additional corridors for each region in case a few corridors could not be used. In addition, an attempt was made to include corridors that covered a range of route types, from heavily urban to more rural and from a variety of areas within each region.

The following corridors were selected for addition to the dataset:

• Omaha-Chicago
• Barstow-Bakersfield
• San Francisco-Portland
• Billings-Sioux Falls
• Chicago-Cleveland
• Amarillo-Oklahoma City
• Detroit-Pittsburgh
• Galveston-Dallas
• San Diego-Los Angeles
• Miami-Atlanta
• Seattle-Billings
• Miami-Richmond
• Seattle-Sioux Falls
• New York City-Cleveland
• Portland-Salt Lake City
• Philadelphia-New York City
• Los Angeles-Tucson
• Dallas-El Paso
• Tucson-San Antonio
• Memphis-Dallas
• Barstow-Salt Lake City
• Memphis-Oklahoma City
• Barstow-Amarillo
• Stouts-Oklahoma City
• Nogales-Tucson
• Seattle-Blaine
• San Antonio-Dallas
• Knoxville-Harrisburg
• Laredo-San Antonio

Having added these corridors, a final regional division was made. Table 13 describes the corridors selected for inclusion in each region.

Table 13. Proposed Final Corridors for Three-Region Analysis

East Region – 18 corridors		Central Region – 18 corridors		West Region – 23 corridors
Atlanta-Jacksonville	ATL-JAX	Amarillo-Oklahoma City	AMA-OKL	Barstow-Amarillo	BAR-AMA
Atlanta-Knoxville	ATL-KNX	Billings-Sioux Falls	BIL-SIO	Barstow-Bakersfield	BAR-BAK
Atlanta-Mobile	ATL-MOB	Chicago-Cleveland	CHI-CLE	Barstow-Salt Lake City	BAR-SAL
Birmingham-Nashville	BGH-NSH	Cleveland-Columbus	CLE-COL	Dallas-El Paso	DAL-ELP
Birmingham-Chattanooga	BIR-CHA	Dayton-Detroit	DAY-DET	Dallas-Houston	DAL-HOU
Detroit-Pittsburgh	DET-PIT	Indianapolis-Chicago	IND-CHI	Denver-Kansas City	DEN-KAN
Harrisburg-Philadelphia	HAR-PHI	Indianapolis-Columbus OH	IND-COL	Denver-Salt Lake City	DEN-SAL
Knoxville-Harrisburg	KNX-HAR	Kansas City-St Louis	KNC-STL	Galveston-Dallas	GAL-DAL
Miami-Atlanta	MIA-ATL	Knoxville-Dayton	KNX-DAY	Laredo-San Antonio	LAR-SAN
Miami-Richmond	MIA-RIC	Louisville-Columbus	COL-LOU	Los Angeles-Tucson	LAX-TUC
Mobile-New Orleans	MOB-NOR	Louisville-Indianapolis	IND-LOU	Nogales-Tucson	NOG-TUC
New Orleans-Birmingham	NOR-BIR	Memphis-Dallas	MEM-DAL	Portland-Salt Lake City	POR-SAL
Boston-New York City	NYC-BOS	Memphis-Oklahoma City	MEM-OKL	Portland-Seattle	POR-SEA
New York City-Cleveland	NYC-CLE	Nashville-Louisville	NSH-LOU	San Antonio-Dallas	SAN-DAL
Harrisburg-New York City	NYC-HAR	Nashville-St Louis	NSH-STL	San Diego-Los Angeles	SDG-LAX
Philadelphia-New York City	PHI-NYC	Omaha-Chicago	OMA-CHI	San Francisco-Los Angeles	SFO-LAX
Columbus-Pittsburgh	PIT-COL	St Louis-Oklahoma City	STL-OKL	San Francisco-Portland	SFO-POR
Richmond-Philadelphia	RIC-PHI	St Louis-Indianapolis	STL-IND	San Francisco-Salt Lake City	SFO-SAL
				San Antonio-Houston	SAN-HOU
				Seattle-Billings	SEA-BIL
				Seattle-Blaine	SEA-BLA
				Seattle-Sioux Falls	SEA-SIO
				Tucson-San Antonio	TUC-SAN

The final regional categorization utilizes a three-region approach. Data availability and quality are the main reasons that a more detailed regional disaggregation has not been pursued.

However, the additive benefit estimation calculator will achieve significantly more specificity to local conditions then the example illustrated herein. This will be achieved though the use of corridor-specific AADTT in the additive benefit calculation and corridor-specific delay characteristics in the transformation of the elasticity estimate.

Additive benefit estimates are provided in this report as an illustration of what the additional reorganization benefit would be for the average corridor in each region. This is not the additional benefit proposed as the addition to every corridor's total benefit estimation. The tool to be developed in a subsequent task will utilize the regional elasticities calculated for this report and corridor-specific data, such as daily truck traffic, current delay, delay reduction, localized cost data, and other locally specific data to develop a corridor-specific additive freight reorganization benefit factor to be applied to calculated freight related benefits.

2.4 Rate, Flow, Commodity, and Performance Data

In addition to adding corridors, the existing dataset was also expanded by adding years of observations. Additional HPMS data collection has occurred since the development of the Phase II dataset. The project team was able to add three years of observations for most corridors, significantly expanding the total number of observations.

Data on heavy-duty vehicle traffic volumes, freight rates, and commodity flows were collected from several different sources. The data used are described below. Note that data on 30 corridors were available from Phase II of this study. Additional years of data were collected for these corridors. Data for 29 new corridors were also collected to enhance the size and regional coverage of our database. Of those 29 corridors, 25 were added to the final sample.

2.4.1 Rate Data

Freight rates for each corridor were obtained from SMC³'s Czarlite[5] database. This database serves as the benchmark for thousands of LTL contracts. Rates were obtained for each corridor using an origin and destination zip code. The rates were defined by using a 1,000 pound, class 70 shipment type to estimate an average rate for each corridor for the years 1993-2004.

2.4.2 Commodity Flow Data

The commodity flows in each corridor were characterized using FAF data from FHWA. Both the original FAF and a newly released version (FAF2) were used since the geographic detail and years available were somewhat different between these databases. The FAF2 database has information on commodity flows between major geographic regions, including some metropolitan area city pairs for the year 2002. Data on the tonnage, value, and commodity types being moved in both directions in the study corridors were developed. Since the geographic regions available in FAF2 did not map exactly to the corridor origin and destination cities used in the analysis, the regions most closely matching this study's corridors were utilized to obtain an approximate picture of existing commodity flows. Commodity flows were developed for 58 distinct corridors and captured information on freight moving in both directions along the corridor.

The original FAF database contains county-to-county movements of freight by commodity type for 1998 and forecast years. Commodity flows for each corridor were developed from this database as well. The purpose of the commodity flow analysis was to understand the differences that exist between the corridors and to develop an understanding of how these differences might affect the results of the modeling.

2.4.3 HPMS

The HPMS Sample database was used to develop information on the average V/C ratios for the corridors being studied. The HPMS Sample database was obtained for the years 1993-2003. Each year of sample data contains approximately 110,000 records. Each record represents one segment and includes data on segment ID, state, county, route number, average annual daily truck traffic, peak and off-peak commercial vehicle percentages, V/C ratio, as well as many other items.

FHWA's list of "freight significant corridors" was used to identify many of the corridors used in this study. Additional corridors were added based on expert judgment or the need to increase regional coverage or include corridor types that were not represented. For instance, a number of major international trade lanes were added to increase the coverage of international commodity flows. A number of rural low-volume freight corridors were added to enhance coverage of this corridor type.

For each corridor identified, the relevant highway routes that would be used between a given city pair were identified. The set of HPMS segments representing these highway routes were then determined. One problem encountered was that, in some cases, routes designated in HPMS would change across years or between states. For instance, in one year a route would be identified as 40, and in another year a route would be identified as I40. There were also variations in how routes were designated between states.

In order to work around this, the data for each state were manually inspected to determine the route designations used for each corridor. Based on this analysis, a list of segments that characterized each corridor was developed.

HPMS data for each study corridor defined were aggregated to develop summary information describing average truck volumes and V/C ratios for each corridor. Truck volumes were obtained by multiplying the off-peak truck percentage by the AADTT for each segment. Corridor averages for truck volumes and V/C ratios were obtained averaging all the segments for each corridor, weighted by the segment length.

A number of problems were encountered. Many segments did not have data for all the years in the analysis. In addition, some segments had zero values in the off-peak truck percentage field. In order to compare data across years for each corridor, it was necessary to eliminate segments from the analysis that did not have data across all years or were missing data. For some corridors, data were unavailable for particular years. In order to address this, the years of data used in each corridor was adjusted to include the most segments, while at the same time making available the largest number of years of data available for analysis.

For example, if most segments were missing for a particular year of data, then that year would be omitted. In some cases, there were duplicate records for some segment IDs. These were dropped from the analysis. A number of corridors that were initially examined did not have enough data available for them. An additional 29 corridors to those used in the national analysis had enough information to develop corridor averages. Table 14 shows the total number of segments available and the number of segments used to develop the data for each of the 29 corridors. Also shown are the years of data that were available for each corridor.

Post data cleaning resulted in 55 corridors, representing both the corridors in the Phase II national analysis and newly added corridors, being usable for our sample.

Table 14. Number of Segments and Years Used to Characterize Each Additional Corridor

Corridor Name	Total Segments	Segments Available for Analysis	Years Covered
Dallas-El Paso	147	141	1997-2000
Memphis-Dallas	148	77	1993-1994 & 1996-2004
Memphis-Oklahoma City	230	70	1993-1994 & 1996-2004
Amarillo-Oklahoma City	155	121	1999-2001
Barstow-Amarillo	371	324	1997-2000
Barstow-Bakersfield	55	48	1994-2000
Barstow-Salt Lake City	234	180	1997-2004
Billings-Sioux Falls	186	140	1993-2004
Denver-Kansas City	111	54	1993-2003
Galveston-Dallas	53	50	1997-2000
Knoxville-Harrisburg	272	224	1996-2004
Laredo-San Antonio	36	34	1997-2000
Los Angeles-Tucson	259	244	1997-2000
Miami-Atlanta	205	163	1998-2002
Miami-Richmond	183	63	1994-2004
Nogales-Tucson	117	92	1996-2000
Philadelphia-NYC	55	16	1997-2002
Pittsburg-Detroit	51	30	1998-2003
Portland-Salt Lake City	365	270	1993-2004
San Antonio-Dallas	111	106	1997-2000
San Diego-Los Angeles	49	39	1994 -2000
Seattle-Billings	212	202	1993-2004
Seattle-Blaine	38	38	1993-2004
Seattle-Sioux Falls	375	321	1993-2004
St. Louis-Oklahoma City	205	194	1999-2002
Tucson-San Antonio	316	248	1996-2000
Chicago-Cleveland	44	16	1996-2004
New York City-Cleveland	683	651	1996-2004
Omaha-Chicago	188	108	1996-2004

2.5 Variables for Regional Discrimination

Having settled on a three-region approach, the project team developed improved variables with greater power for regional discrimination for inclusion in the original equations. These included replacement of GDP as the variable used to describe economic growth with Gross State Product (GSP), which was developed by selecting from the states in which the corridors begin and end. Use of GSP allowed for improved discrimination between regions by better tying performance improvements to local economic growth. National Producer Price Index (PPI) inputs, used for discounting income and truck rate variables, were replaced with localized Consumer Price Index (CPI) numbers developed by the Bureau of Economic Analysis.

Rate-data specific to each corridor, traffic flows, and capacity information provide the key corridor-level discrimination. The addition of regional economic variables enhances the ability of the model to distinguish between regions.

Table 15 describes some of the key characteristics of each region given the improved dataset.

Table 15. Descriptive Statistics of Corridors by Region

	Region	Average	Minimum	Maximum
Daily Truck Flows	All Corridors	6,133	642	12,731
	East Coast Corridors	7,113	642	12,433
	Midwest Corridors	6,835	789	12,731
	West Coast Corridors	4,666	1,726	8,338
Population	All Corridors	4,445,071	392,572	16,971,055
	East Coast Corridors	4,554,063	448,948	10,035,145
	Midwest Corridors	2,836,174	392,572	9,154,470
	West Coast Corridors	5,869,570	2,184,897	16,971,055
Per capita income '000 (real)	All Corridors	18.122	12.403	26.079
	East Coast Corridors	19.284	14.571	26.079
	Midwest Corridors	17.617	14.228	20.842
	West Coast Corridors	17.642	12.403	21.056
LTL Rates per mile (real)	All Corridors	0.615	0.165	1.902
	East Coast Corridors	0.749	0.217	1.902
	Midwest Corridors	0.654	0.256	1.368
	West Coast Corridors	0.472	0.165	1.684

2.6 Measuring Highway Performance

A primary requirement of the analysis methodology used to estimate the reorganization effect is to relate the demand for trucking and the rates that carriers charge shippers to a measure of highway performance. Although there are numerous measures that could be employed for this purpose (such as level-of-service indices), prior study suggests that the V/C ratio can serve as a reliable proxy to facility performance.[6]

Consequently, in this study, highway performance variables include V/C ratios and measures of delay along the corridors that are included in this analysis. In HPMS, V/C ratios represent the 30th busiest hour during a given year for a particular segment. V/C ratios for the corridors were estimated by taking the weighted average of the V/C ratios measured along individual segments (the length of the segments was used as the weight). Per-mile delay for a given corridor is the weighted average of all the delays on segments along the corridor.

Delay data were estimated by using the V/C ratios for selected segments and by estimating free flow and congested flow travel times. First, travel time on each segment was estimated assuming free flow of the traffic. Next, travel time with congestion was estimated as follows.

The model applies a standard equation to derive actual (congested) speed from information on the V/C ratio and free flow speed. Two equations were considered and tested:

1. The Bureau of Public Roads (BPR) equation:
   
   Congested Speed = (Free-Flow Speed) / (1 + 0.15 * [volume/capacity] ^ 4)
2. The Metropolitan Transportation Commission (MTC) equation:
   
   Congested Speed = (Free-Flow Speed) / (1 + 0.20 * [volume/capacity] ^ 10)

Finally, the difference between free-flow travel time and congested travel time is assumed to be the delay on this segment. The total delay figures were divided by the total length of the segments to estimate delay per mile as a highway performance measure for these corridors.

One approach considered, and then rejected, was not using a weighted average for delay per mile. A non-weighted approach would have the advantage of emphasizing the degree of delay in the highly congested segments of the corridor.

The weighted average approach is used in an attempt to describe the characteristics of an entire corridor. AADTT is the aggregate of the corridor segments. Therefore a delay factor that is also descriptive of the entire corridor is needed. By not weighting the delay by segment length, one would be vulnerable to accusations of over-valuing the portion of the corridor that is highly delayed and thereby over-valuing the relationship between performance improvements or reductions and demand.

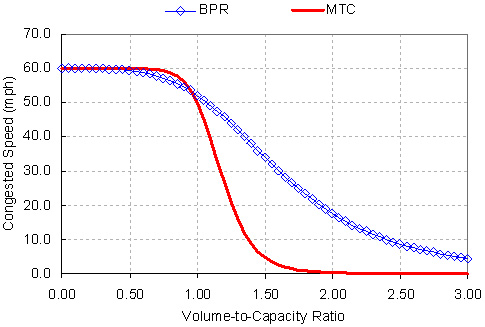
Figure 3. Assumed Speed-Flow Relationships

Note: Assumes a free-flow speed of 60 mph.

You will need the Adobe Reader to view the PDFs on this page.

previous | next