3. Empirical Results

3.1 Estimating Regional Elasticities of Demand

Chapter 2 described tests employed to select a geographic division. Based on the tests and empirical results achieved, the project team selected an approach for estimating the elasticity of demand with respect to highway performance. This section describes and reports the results obtained.

The following equation was estimated separately for each region (East, Central, and West), when demand for daily truck traffic is specified as a function of delay and real per capita income growth:

Log(AADTT_c,t) = β_c + β₁Delay_c,t + β₂Income_c,t

where:

AADTT = Average annual daily truck traffic
Delay = Average delay per mile
Income = Real per capita income growth
t = 1993, 1994,… 2003
c = Corridor

β_c are corridor-specific constant, or fixed effects, where:

c = 1,…, 16 for East,
c = 1,…, 18 for Central,
c = 1,…, 21 for West

The coefficientβ₁ from the log-lin specification of the model above might be transformed into the elasticity coefficient. In calculus notation,β₁ can be expressed as

,

And since the elasticity coefficient (elasticity of demand with respect to highway performance-delay) is defined as

,

Therefore

.

The regression results are summarized in Tables 16, 17, and 18 for the East, Central, and West regions, respectively. The models explain a high percentage of variability in freight demand measured by average annual daily truck traffic, at about 79% for the East, 95% for the Central, and about 94% for the West.

The coefficients on the delay and income variable have the correct signs and are statistically significant. The only exception is the coefficient on income in the model for the West region (see Table 18), which is insignificant at the 5% level. However, it is significant at the 10% level.

Table 16. Regression Results for the East Region

Dependent Variable: LOG(AADTT)
Method: Pooled EGLS (Cross-section weights)
Total pool (unbalanced) observations: 114
Variable	Coefficient	Std. Error	t-Statistic	p-value
Constant	8.847002	0.013168	671.8803	0.0000
Delay	-0.005117	0.002344	-2.182555	0.0315
Real Per Capita Income Growth	0.008595	0.004069	2.112079	0.0373
Fixed Effects:
Atlanta-Jacksonville	0.125424
Atlanta-Knoxville	0.323139
Atlanta-Mobile	-0.233984
Birmingham-Nashville	-0.232907
Columbus-Pittsburgh	-0.054241
Harrisburg-Philadelphia	0.012104
Mobile-New Orleans	-0.259956
Richmond-Philadelphia	0.44495
Boston-New York City	0.032609
Harrisburg-New York City	0.154785
Detroit-Pittsburgh	-0.104274
Philadelphia-New York City	-0.106916
New York City-Cleveland	0.037953
Miami-Richmond	-0.261302
Miami-Atlanta	-0.176157
Knoxville-Harrisburg	0.297654
R-squared	0.78757	Mean dependent var		8.856317
Sum squared resid	1.534467	Durbin-Watson stat		1.020177

Table 17. Regression Results for the Central Region

Dependent Variable: LOG(AADTT)
Method: Pooled EGLS (Cross-section weights)
Total pool (unbalanced) observations: 138
Variable	Coefficient	Std. Error	t-Statistic	p-value
Constant	8.745927	0.011244	777.8526	0.0000
Delay	-0.069076	0.019921	-3.467458	0.0007
Real Per Capita Income Growth	0.00866	0.003502	2.473205	0.0148
Fixed Effects:
Cleveland-Columbus	0.187098
Dayton-Detroit	0.127923
Indianapolis-Chicago	0.176353
Indianapolis-Columbus	0.345631
Kansas City-St Louis	0.192902
Knoxville-Dayton	0.322572
Louisville-Columbus	0.231423
Louisville-Indianapolis	0.198499
Nashville-Louisville	0.598196
Nashville-St Louis	-0.398262
St Louis-Indianapolis	0.189179
Omaha-Chicago	0.01184
Chicago-Cleveland	-0.206494
Billings-Sioux Falls	-1.651534
Amarillo-Oklahoma City	0.142811
Memphis-Dallas	0.373809
Memphis-Oklahoma City	0.165234
St Louis-Oklahoma City	-0.349393
R-squared	0.948179	Mean dependent var		8.744014
Sum squared resid	2.002249	Durbin-Watson stat		1.010586

Table 18. Regression Results for the West Region

Dependent Variable: LOG(AADTT)
Method: Pooled EGLS (Cross-section weights)
Total pool (unbalanced) observations: 129
Variable	Coefficient	Std. Error	t-Statistic	p-value
Constant	8.370945	0.011247	744.2735	0.0000
Delay	-0.015586	0.00573	-2.720287	0.0076
Real Per Capita Income Growth	0.005534	0.003323	1.665585	0.0987
Fixed Effects:
Dallas-Houston	0.533012
San Antonio-Houston	0.335623
Denver-Kansas City	-0.672123
Denver-Salt Lake City	0.044107
San Francisco-Salt Lake City	-0.632347
San Francisco-Los Angeles	0.247815
Portland-Seattle	0.668379
San Diego-Los Angeles	0.544992
Seattle-Billings	-0.6264
Seattle-Sioux Falls	-0.867802
Portland-Salt Lake City	-0.276968
Los Angeles-Tucson	0.097899
Tucson-San Antonio	0.557139
Laredo-San Antonio	-0.06466
Nogales-Tucson	0.28696
San Antonio-Dallas	0.669072
Barstow-Bakersfield	0.257096
Barstow-Amarillo	0.105583
Barstow-Salt Lake City	-0.156777
Galveston-Dallas	0.343733
Dallas-El Paso	0.198615
R-squared	0.940778	Mean dependent var		8.377655
Sum squared resid	1.913074	Durbin-Watson stat		0.776213

The semi-logarithmic functional form of the estimated equations requires the coefficients on the delay variable to be transformed in order to interpret them in elasticity terms. Table 19 shows this step and provides a summary of findings regarding the impact of changes in delay on freight demand.

Table 19. Implied Elasticity of Demand for Three Regions

Region	Coefficient on Delay	Implied Elasticity	Interpretation
East	-0.005117	-0.0076	Other things being equal, a 10% increase in delay per mile reduces freight demand by 0.07%.
Central	-0.069076	-0.0175	Other things being equal, a 10% increase in delay per mile reduces freight demand by 0.175%.
West	-0.015586	-0.0070	Other things being equal, a 10% increase in delay per mile reduces freight demand by 0.07%.

3.2 Calculating Regional Additive Freight Reorganization Benefits

3.2.1 Microeconomic Framework

Figure 4 gives a diagrammatic representation of the microeconomic framework which identifies the benefits of industrial reorganization. Area A represents the immediate benefits of a highway improvement to existing highway users (principally user time savings and reduced vehicle operating costs). Area B represents the immediate benefits accruing to users newly attracted to the highway by virtue of the improvement. Areas A and B together represent the benefits conventionally measured in a CBA.

Area C represents the value of efficiency gains to the economy due to industrial reorganization precipitated by the highway improvement. Industrial reorganization means the adoption of advanced logistics the firm's business case for which depend on the likelihood of a threshold level of reliability in highway performance. Defined as the ratio of area C to the sum of areas A and B namely,C/[A+B] expressed as a percentage, the "additive freight reorganization benefit" gives the percentage by which to increase the value of conventionally-measured benefits to freight traffic in order to approximate total benefits. In other words, the benefits inclusive of the reorganization effect.

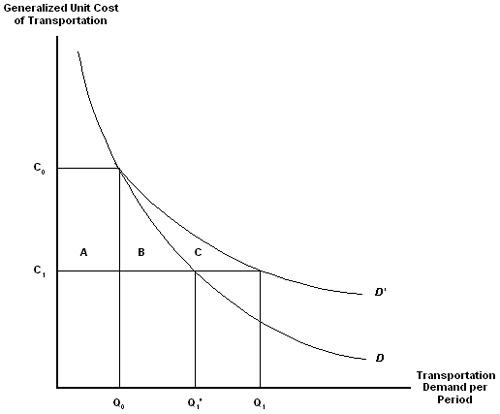
Figure 4. Change in Consumer Surplus from Changing Demand for Transportation as a Function of Unit Generalized Transportation Cost

To assess the quantitative significance of the additive reorganization benefit, the study amassed quantitative evidence of the following:

Q₀: Initial demand for freight transportation (vehicle-miles (vm));
Q₁: New demand level as a result of highway improvements or policy change;
C₀: Initial unit generalized cost of transportation ($/vm);
C₁: New unit generalized cost of transportation ($/vm) following highway improvement or policy change; and
β₀ β₁ Immediate and post-reorganization slopes of the transport demand curves (respectively) with respect to the generalized cost of transportation, where generalized cost is the linear sum of vehicle operating expenses, delay-related expenses and unreliability-related expenses.

As discussed in the Phase II report on the national analysis, a variable-elasticity form of the present and post-reorganization demand curves (indicating constant returns to scale) provides a reasonable description of the available data. Specifically, the elasticity of demand for transport with respect to generalized cost is found to vary proportionately with generalized cost. This means that the elasticity is smaller when generalized cost is relatively low, and it is higher when generalized cost is relatively high, implying that demand is more sensitive to changes in highway conditions when congestion is high than when congestion is low. The form of the estimated demand curve is:

Ln Q = β₀ + β₁ * C

where Q is the quantity of transportation that would be demanded at a generalized cost of C, and whereβ₀ andβ₁ are constants estimates with least-squares in a fixed-effects model that controls for between-corridor variations.

3.2.2 Additive Benefit Calculation Module

The additive benefit estimation module has been developed to accommodate outcomes from two broad categories of cost benefit analysis models: 1) standard user cost models, where the practitioner focuses on the reduction of user costs to existing highway users (baseline transportation demand, as measured by truck vehicle miles traveled (VMT) or other metrics) and ignore induced demand (additional highway trips brought about by the reduction in transport costs); and 2) consumer surplus models, where the practitioner explicitly accounts for induced demand using standard transportation demand elasticity estimates and estimates the change in consumer surplus resulting from a candidate highway investment.

Additive Benefit Estimation with Standard User Cost Models

In Figure 5, the additive benefit would be estimated as the ratio of indirect benefits, represented by the red triangle B (the area between the long run transport demand curve and theC₁ line, and bounded byVM₀ andVM₁), to direct benefits, represented by the blue rectangle A (the area between theC₀ andC₁ lines and to the left ofVM₀).

Additive Benefit Factor = Area B / Area A

With the application of the additive benefit factor, direct benefits (or benefits to existing highway users) are augmented to represent total benefits (direct plus indirect benefits). Total benefits within this framework are measured by the change in consumer surplus using the long-run demand curve for freight.

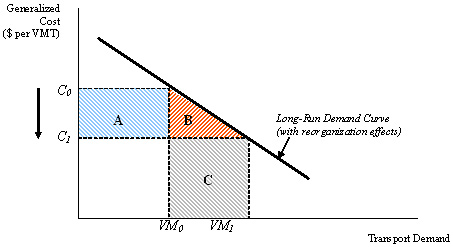
Figure 5. Additive Benefit Estimation with Standard User Cost Models, An Illustration

A numerical example of additive freight reorganization benefit estimation is provided in Table 20.

Table 20. Additive Benefit Estimation with Standard User Cost Models, A Numerical Example

#	Parameters	Value	Comments
Unit Generalized Costs ($/vehicle mile)
1	C0	$3.8100	Assumption / input.
2	C1	$3.4351	Assumption (10% reduction).
Transport Demand (freight vehicle miles)
3	VM0	200,000	Assumption / input.
4	VM1	220,434*	Calculated using the nominal elasticity (b).
Demand Curve
5	Constant(a = VM0*C0 raised to power b)	49,879
6	Full Price Elasticity (b)	-1.0382*
7	r = 1-(1/b)	1.9632	Estimation of area below demand curve and betweenVM0 andVM1.
8	a^(1/b)	2.98484E-05
9	a^(1/b) * ((VM1^r)-(VM0^r))/r	81,679
10	Delta VM * C1	70,191	Estimation of area D.
11	VM0 * Delta C	74,988	Estimation of area A.
12	Direct Benefits (Row 11)	$74,988	User cost savings.
13	Indirect Benefits (Row 9 minus Row 10)	$11,487	Estimation of area B (triangle).
14	Total benefits (Row 12 + Row 13)	$86,476	Area A + B.
15	% Indirect / Direct	15.3%*	The additive benefit factor.

*Numbers in red signify key variables that illustrate the change in demand.

The full price elasticity (b) on row 6 is estimated by considering the combined impact of the elasticity of demand with respect to out-of-pocket costs (direct vehicle operating costs or shipping rate) and a measure of the long-run elasticity of demand with respect to highway performance (transit time and reliability).

For the purpose of this study, the elasticity of freight demand with respect to transportation costs was derived from the literature (-0.97, Tae Oum). The long-run elasticity of demand with respect to highway performance was estimated econometrically, as part of Phase II and Phase III of the study.

Additive Benefit Estimation with Consumer Surplus Models

In Figure 6, the additive benefit factor would be calculated as the ratio of area F (the area between the long-run transport demand curve "with reorganization effects," the standard short run demand curve, and theC1 line) to a standard measure of consumer surplus, represented by area A plus area E.

Additive Benefit Factor = Area F / (Area A + Area E)

In other words, the additive benefit factor is estimated as the percentage change in consumer surplus resulting from incremental transport demand along the long-run demand curve. Incremental transport demand is illustrated by the shift fromVM₁ toVM₂ on Figure 6.

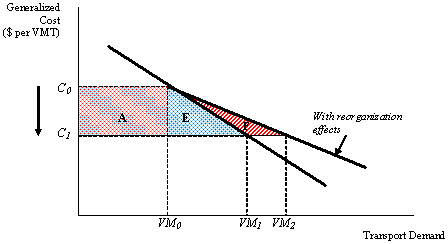
Figure 6. Additive Benefit Estimation with Consumer Surplus Models, An Illustration

A numerical example of additive benefit estimation with consumer surplus models is provided in Table 21.

Table 21. Additive Benefit Estimation with Consumer Surplus Models, A Numerical Example

#	Parameters	Standard Consumer Surplus Model Output	Augmented Output and Additive Benefit Estimation
Unit Generalized Costs ($/vehicle mile)
1	C0	$3.8100	$3.8100
2	C1	$3.4351	$3.4351
Transport Demand (freight vehicle miles)
3	VM0	200,000	200,000
4	VM1	219,400*	220,434*
Demand Curve
5	Constant(a = VM0*C0 raised to power b)	54,642	49,879
6	Full Price Elasticity (b)	-0.9700*	-1.0382*
7	r = 1-(1/b)	2.0309	1.9632
8	a^(1/b)	1.30602E-05	2.98484E-05
9	a^(1/b) * ((VM1 or 2^r)-(VM0^r))/r	77,614	81,679
10	Delta VM * C1	66,641	70,191
11	VM0 * Delta C	74,988	74,988
12	Direct Benefits (Row 11)	$74,988	$74,988
13	Indirect Benefits (Row 9 minus Row 10)	$10,973	$11,487
14	Total benefits (Row 12 + Row 13)	$85,962	$86,476
15	% change in "total benefits"		0.60%*
16	% change in "indirect benefits"		4.7%*

*Numbers in red signify key variables that illustrate the change in demand.

Discussion

Both approaches may be developed for the Phase III tool so that analysts not estimating user costs prior to calculator use would still be able to calculate an additive freight reorganization benefit factor. A review of current CBA approaches suggests that most analysts would likely use the Consumer Surplus approach.

In both models, the calculation is sensitive to the difference between current and anticipated demand (AADTT) and user costs, which are items that will vary project to project. It is proposed that the model also calculate the transformation of the elasticity on a project-by-project basis, factoring in the existing delay on the segment being improved. This would also add variability and local specificity to the additive benefit calculation.

Both approaches will be further assessed and refined as part of Phase III-B.

3.2.3 Regional Additive Benefit Factors

The process of computing the additive benefit factor, explained above, was then applied to the three regions of interest. Each region is defined by its elasticities of demand with respect to performance and price.

Table 22 shows the regional elasticities of demand with respect to highway performance estimated through regression analysis in earlier steps.

Table 22. Elasticity of Demand with Respect to Highway Performance

Region	Implied Elasticity
East	-0.0076
Central	-0.0175
West	-0.007

Several difficulties were encountered in Phase II for the development of price elasticity. Both price and demand elasticity are required for the estimation of an additive benefit factor. One acknowledged and accepted value for price elasticity (derived from estimates by Tae Oum in a national analysis is currently used for each of the three corridors. Therefore the value of -.97, as estimated by Tae Oum, is used here. However, an attempt was made to regionalize this value as follows:

Table 23. Elasticity of Demand with Respect to Price

U.S.	Regional Differences* When Compared to the National Level (-0.97 = 100%)		Regional Estimate of Elasticity of Demand with Regard to Price
	East	115.3%	East	-1.12
-0.97	Central	99.6%	Central	-0.97
	West	86.9%	West	-0.84

Using the two elasticities presented above and the computer model described above, sample regional additive benefit factors were calculated, as shown in Table 24. These represent an additive benefit factor for the typical corridor in each regional sample and are provided as an illustration of the additional freight benefits would have been for the average corridor in each region.

Each corridor developing a logistics benefit estimation will derive a unique additive benefit factor based on certain regional and national characteristics:

• Regional elasticity
• Price elasticity

And certain corridor-specific characteristics:

• AADTT
• Delay
• Predicted traffic demand
• User costs
• Calculated freight benefits

Table 24. Regional Additive Benefit Factors

Region	East	Central	West
Additive Benefit Factor	16.7%	14.8%	12.7%

3.2.4 Commodity Flow Data Analysis

Analysis of FAF commodity flow data was conducted for the East, Central, and West regions. Data available included top commodities by volume (weight) and by value. The data describe regional mixes of freight movement that are similar but not the same.

From a value perspective, finished and semi-finished goods rank high in the mix of goods in each region; however, the specific goods vary by region. Except for the Central region, finished goods were not significant contributors of freight volume. In the Central region, machinery and motorized vehicles were the ninth and tenth largest categories of shipment by volume.

Tables 25 and 26 present the top commodities by thousand tons and dollar value. This greater than average volume of finished and semi-finished goods in the Central region may explain the higher than average elasticity of demand with respect to highway performance in the region.

Table 25. Top Commodities Transported in Three Regions (Thousand Tons)

Region	Commodity	Thousand Tons
East	Gravel	7,173.3
	Waste/scrap	5,999.1
	Cereal grains	5,110.0
	Other foodstuffs	4,083.3
	Unknown	3,956.9
	Nonmetal mineral products	3,576.3
	Wood prods.	3,154.3
	Mixed freight	3,024.1
	Base metals	2,916.3
	Nonmetallic minerals	2,322.5
Central	Base metals	2,866.0
	Nonmetal mineral products	2,480.8
	Gasoline	2,013.9
	Other foodstuffs	1,795.7
	Mixed freight	1,621.7
	Unknown	1,587.5
	Waste/scrap	1,471.8
	Gravel	1,385.6
	Machinery	1,164.6
	Motorized vehicles	1,115.2
West	Nonmetal mineral products	14,739.6
	Gravel	7,703.2
	Gasoline	7,593.5
	Coal, n.e.c.	4,344.5
	Mixed freight	3,707.7
	Other foodstuffs	3,488.1
	Unknown	3,415.4
	Wood prods.	3,136.2
	Natural sands	2,623.0
	Waste/scrap	2,491.3

Table 26. Top Commodities Transported in Three Regions ($Million)

Region	Commodity	$M
East	Mixed freight	11,824
	Machinery	10,247
	Motorized vehicles	6,054
	Textiles/leather	5,047
	Pharmaceuticals	4,891
	Other foodstuffs	4,399
	Electronics	3,951
	Printed prods.	3,788
	Unknown	3,690
	Misc. manufacturing products	3,457
Central	Machinery	7,420
	Mixed freight	6,568
	Motorized vehicles	5,306
	Base metals	2,672
	Pharmaceuticals	2,618
	Electronics	2,159
	Articles-base metal	1,907
	Misc. manufacturing products	1,877
	Other foodstuffs	1,826
	Plastics/rubber	1,623
West	Mixed freight	17,672
	Machinery	13,279
	Electronics	13,224
	Motorized vehicles	8,732
	Other foodstuffs	5,366
	Textiles/leather	5,303
	Chemical prods.	4,811
	Articles-base metal	4,807
	Gasoline	4,582
	Misc. manufacturing products	4,322

previous | next